Musings, Courses, & Projects by Rob Marano

Notes for Week 3

← back to syllabus ← back to notes

Topics

  1. Verilog: Parameterization; Built-in primitives; User-defined primitives; Dataflow modeling
  2. Stored Program Concept
  3. History of computer architecture and modern advancements

Topics Deep Dive

More on Verilog

Parameterize Your Verilog Code

Parameters are fundamental for creating reusable and configurable hardware designs. They allow you to define constants that can be modified at compile time, influencing the behavior and structure of your modules. Think of them as global variables within a module’s scope, but with the crucial difference that they are typically resolved before simulation.

Let’s break down how to use parameters effectively in SystemVerilog.

1. Declaring Parameters:

You declare a parameter using the parameter keyword. The basic syntax is:

parameter [data_type] parameter_name = value;

Some examples:

parameter WIDTH = 8; // An 8-bit wide value
parameter DEPTH = 256; // A depth value
parameter REAL_VAL = 3.14159; // A real value
parameter logic [7:0] DEFAULT_VALUE = 8'hAA; // An 8-bit logic value
parameter enum { STATE_IDLE, STATE_READ, STATE_WRITE } STATE = STATE_IDLE; // Enumerated type

2. Using Parameters:

Once declared, you can use parameters anywhere within the module where a constant value is required. This includes:

For example, a parameterized adder using behavioral modeling

module adder #(parameter WIDTH = 8) (
  input logic [WIDTH-1:0] a,
  input logic [WIDTH-1:0] b,
  input logic cin,
  output logic [WIDTH-1:0] sum,
  output logic cout
);

  assign {cout, sum} = a + b + cin;

endmodule

Using the adder in other modules, like a test bench.

// code below would be in a test bench or another module's definition.
// Instantiating the adder with different widths:
adder #(.WIDTH(16)) adder16 (
  .a(data_a),
  .b(data_b),
  .cin(carry_in),
  .sum(sum16),
  .cout(carry_out)
);

adder adder8 ( // Using the default WIDTH = 8
  .a(data_c),
  .b(data_d),
  .cin(carry_in2),
  .sum(sum8),
  .cout(carry_out2)
);

3. Overriding Parameters:

The real power of parameters comes from the ability to override their values during module instantiation. This is done using the #(.parameter_name(value)) syntax, as shown in the adder example above. This allows you to reuse the same module with different configurations without modifying the module’s source code.

4. Local Parameters:

SystemVerilog also provides the keyword localparam. These are similar to parameters but cannot be overridden during instantiation. They are strictly local to the module in which they are defined. Use localparam for constants that should not be changed externally.

localparam DELAY = 2; // A delay value that should not be modified from outside

Key Advantages of Using Parameters:

Best Practices:

Programmatically Generate Circuits

Generate blocks provide a mechanism for creating multiple instances of modules or code blocks based on compile-time conditions or loop iterations. This is essential for designing regular structures like arrays of processing elements, memory banks, or replicated logic. genvar is a special variable used exclusively within generate blocks as an index or iterator.

1. The genvar Keyword:

genvar declares an integer variable that is used as a loop counter or index within a generate block. It’s crucial to understand that genvar is not a regular variable; it exists only during the elaboration phase (before simulation) and is used to generate hardware instances. You cannot use a genvar outside of a generate block.

genvar i; // Declaring a genvar

2. The generate Block:

Reference-1

Reference-2

The generate block encloses the code that you want to replicate or conditionally instantiate. There are three main types of generate constructs:

3. for Loop Generate:

This is the most common type. It’s used to create multiple instances of a module or block of code.

generate
  for (genvar i = 0; i < N; i++) begin : instances // 'instances' is a generate block name (important!)
    // Inside the loop, 'i' is used to create unique instances.
    adder #( .WIDTH(WIDTH) ) adder_inst (
      .a(data_a[i*WIDTH+:WIDTH]), // Using 'i' to index into a wider data bus
      .b(data_b[i*WIDTH+:WIDTH]),
      .cin(carry_in[i]),
      .sum(sum[i*WIDTH+:WIDTH]),
      .cout(carry_out[i])
    );
  end
endgenerate

4. if-else Generate:

This construct allows you to conditionally instantiate different blocks of code based on a compile-time condition.

generate
  if (ENABLE_ADDER) begin : adder_block
    adder #( .WIDTH(WIDTH) ) adder_inst (
      .a(data_a),
      .b(data_b),
      .cin(carry_in),
      .sum(sum),
      .cout(carry_out)
    );
  end else begin : multiplier_block
    multiplier #( .WIDTH(WIDTH) ) multiplier_inst (
      .a(data_a),
      .b(data_b),
      .prod(product)
    );
  end
endgenerate

5. case Generate:

Similar to if-else, but for multiple conditions.

generate
  case (OPERATION)
    ADD: begin : add_block
      // ... instantiation for addition ...
    end
    SUBTRACT: begin : sub_block
      // ... instantiation for subtraction ...
    end
    default: begin : default_block
      // ... default instantiation ...
    end
  endcase
endgenerate

Important Considerations:

For example, Parameterized Memory Array:

module memory_array #(
  parameter DEPTH = 256,
  parameter WIDTH = 8
) (
  // ... ports ...
);

  genvar i;
  generate
    for (i = 0; i < DEPTH; i++) begin : memory_instances
      memory_cell #( .WIDTH(WIDTH) ) mem_cell (
        // ... connections ...
      );
    end
  endgenerate

endmodule

This example creates an array of DEPTH memory cells, each of WIDTH bits.

Conclusion Using genvar and generate

By mastering generate blocks and genvars, you can create highly parameterized and reusable hardware designs, significantly improving your productivity and code maintainability. Now, let’s put this knowledge into practice with some exercises!

Let’s create a variable bit length Register File

Step 1 — The D flip-flop with reset and enable signals:

The dff module:

module dff (
  input logic clk,
  input logic rst,
  input logic enable,
  input logic d,
  output logic q
);

  always_ff @(posedge clk) begin
    if (rst) begin
      q <= 0; // Synchronous reset
    end else if (enable) begin
      q <= d; // Data is loaded only when enable is high
    end
  end

endmodule

The test bench for the dff module:

// Testbench to demonstrate the d_flip_flop
module d_flip_flop_tb;
  logic clk;
  logic rst;
  logic enable;
  logic d;
  logic q;

  d_flip_flop dut (
    .clk(clk),
    .rst(rst),
    .enable(enable),
    .d(d),
    .q(q)
  );

  // Clock generation
  initial begin
    clk = 0;
    forever #5 clk = ~clk; // 10ns period
  end

  // Test sequence
  initial begin
    rst = 1;
    enable = 0;
    d = 0;

    #10 rst = 0; // Release reset

    d = 1;
    enable = 1;
    #10; // q should now be 1

    d = 0;
    enable = 1;
    #10; // q should now be 0

    enable = 0; // Disable the flip-flop
    d = 1;      // Change d, but q should remain unchanged
    #10;       // q should still be 0

    enable = 1; // Enable again
    #10;       // q should now be 1

    $display("Final value of q: %b", q);
    $finish;
  end

endmodule

Step 2 — The Register

The register module:

module register #(
  parameter WIDTH = 8 // Default width of 8 bits
) (
  input logic clk,
  input logic rst,
  input logic enable,
  input logic [WIDTH-1:0] d, // Data input, parameterized width
  output logic [WIDTH-1:0] q // Data output, parameterized width
);

  // Array of D flip-flops to form the register
  logic [WIDTH-1:0] q_internal; // Internal storage for the register

  genvar i;
  generate
    for (i = 0; i < WIDTH; i++) begin : flip_flops
      dff flip_flop_inst (
        .clk(clk),
        .rst(rst),
        .enable(enable),
        .d(d[i]),      // Connecting individual bits of d
        .q(q_internal[i]) // Connecting individual bits of q_internal
      );
    end
  endgenerate

  assign q = q_internal; // Assign the internal storage to the output

endmodule

The test bench for the register module:

// Testbench for the parameterized register
module register_tb;
  logic clk;
  logic rst;
  logic enable;
  logic [7:0] d; // 8-bit data for default instantiation
  logic [7:0] q;

  // Instantiating the register with the default width (8 bits)
  register reg8 (
    .clk(clk),
    .rst(rst),
    .enable(enable),
    .d(d),
    .q(q)
  );

  // Instantiating the register with a different width (16 bits)
  logic [15:0] d16;
  logic [15:0] q16;
  register #( .WIDTH(16) ) reg16 ( // Parameter override
    .clk(clk),
    .rst(rst),
    .enable(enable),
    .d(d16),
    .q(q16)
  );


  // Clock generation
  initial begin
    clk = 0;
    forever #5 clk = ~clk;
  end

  // Test sequence
  initial begin
    rst = 1;
    enable = 0;
    d = 8'hAA; // Example data for 8-bit register
    d16 = 16'hBEEF; // Example data for 16-bit register

    #10 rst = 0;  // Release reset
    enable = 1;

    #10 d = 8'h55; // Change data for 8-bit register
    #10 d16 = 16'hDEAD; // Change data for 16-bit register

    #10 enable = 0; // Disable

    #10 enable = 1; // Enable again

    #10 $display("8-bit Register q: %h", q); // Should be 55
    #10 $display("16-bit Register q16: %h", q16); // Should be DEAD

    $finish;
  end

endmodule

Step 3 — The Register File

The register_file module:

module register_file #(
  parameter DEPTH = 8,  // Number of registers (default 8)
  parameter WIDTH = 8   // Width of each register (inherited or specified)
) (
  input logic clk,
  input logic rst,
  input logic enable,

  input logic [$log2(DEPTH)-1:0] write_addr, // Write address
  input logic [WIDTH-1:0] write_data,      // Write data
  input logic write_en,                  // Write enable

  input logic [$log2(DEPTH)-1:0] read_addr1, // Read address 1
  output logic [WIDTH-1:0] read_data1,     // Read data 1

  input logic [$log2(DEPTH)-1:0] read_addr2, // Read address 2
  output logic [WIDTH-1:0] read_data2      // Read data 2
);

  // Array of registers
  register #( .WIDTH(WIDTH) ) registers [DEPTH]; // Parameterized register instances

  genvar i;
  generate
    for (i = 0; i < DEPTH; i++) begin : register_instances
      registers[i] (
        .clk(clk),
        .rst(rst),
        .enable(enable),
        .d( (write_en && (write_addr == i)) ? write_data : '0 ), // Conditional write
        .q() // Output not directly connected within the array
      );
    end
  endgenerate

  // Read logic (combinational) - Two independent read ports
  assign read_data1 = registers[read_addr1].q; // Hierarchical access to register output
  assign read_data2 = registers[read_addr2].q; // Hierarchical access to register output

endmodule

The test bench for the register_file module:

// Testbench for the parameterized register file
module register_file_tb;
  logic clk;
  logic rst;
  logic enable;

  logic [2:0] write_addr; // 8 registers so 3 bits for address
  logic [7:0] write_data;
  logic write_en;

  logic [2:0] read_addr1;
  logic [7:0] read_data1;

  logic [2:0] read_addr2;
  logic [7:0] read_data2;

  register_file rf (
    .clk(clk),
    .rst(rst),
    .enable(enable),
    .write_addr(write_addr),
    .write_data(write_data),
    .write_en(write_en),
    .read_addr1(read_addr1),
    .read_data1(read_data1),
    .read_addr2(read_addr2),
    .read_data2(read_data2)
  );

  // Clock generation
  initial begin
    clk = 0;
    forever #5 clk = ~clk;
  end

  // Test sequence
  initial begin
    rst = 1;
    enable = 0;
    write_en = 0;

    #10 rst = 0;
    enable = 1;

    write_addr = 3'h3;
    write_data = 8'hAA;
    write_en = 1;
    #10 write_en = 0;

    write_addr = 3'h5;
    write_data = 8'h55;
    write_en = 1;
    #10 write_en = 0;

    read_addr1 = 3'h3;
    read_addr2 = 3'h5;

    #10;

    $display("Read Data 1 (addr 3): %h", read_data1); // Should be AA
    $display("Read Data 2 (addr 5): %h", read_data2); // Should be 55

    $finish;
  end

endmodule

How about counters?

Simple Counter

The counter module:

module counter #(
  parameter WIDTH = 8 // Default width of 8 bits
) (
  input logic clk,
  input logic rst,
  input logic enable,
  output logic [WIDTH-1:0] count
);

  logic [WIDTH-1:0] count_internal; // Internal storage for the counter

  always_ff @(posedge clk) begin
    if (rst) begin
      count_internal <= '0; // Reset to 0
    end else if (enable) begin
      count_internal <= count_internal + 1; // Increment on rising clock edge when enabled
    end
  end

  assign count = count_internal; // Assign internal value to output

endmodule

The test bench for the counter module:

// Testbench for the counter
module counter_tb;
  logic clk;
  logic rst;
  logic enable;
  logic [7:0] count; // 8-bit count for default instantiation

  // Instantiate the counter (default 8-bit width)
  counter counter_8bit (
  .clk(clk),
  .rst(rst),
  .enable(enable),
  .count(count)
  );

  // Instantiate a 16-bit counter to test parameter override
  logic [15:0] count_16bit;
  counter #(16) counter_16bit_inst ( // Override WIDTH to 16
  .clk(clk),
  .rst(rst),
  .enable(enable),
  .count(count_16bit)
  );


  // Clock generation
  initial begin
    clk = 0;
    forever #5 clk = ~clk; // 10ns period
  end

  // Test sequence
  initial begin
    rst = 1;
    enable = 0;

    #10 rst = 0; // Release reset
    enable = 1;

    #10;      // count should be 1 (8-bit) and 1 (16-bit)
    #10;      // count should be 2 (8-bit) and 2 (16-bit)
    #10;      // count should be 3 (8-bit) and 3 (16-bit)

    $display("8-bit Count: %h", count);      // Should be 3
    $display("16-bit Count: %h", count_16bit); // Should be 3

    // Test overflow for 8-bit counter
    repeat (253) @(posedge clk); // Count up to 255
    #10;
    $display("8-bit Count (Overflow): %h", count); // Should be FF (255)
    #10;
    $display("8-bit Count (After Overflow): %h", count); // Should be 00 (wrapped around)

    // Test overflow for 16-bit counter
    repeat (65533) @(posedge clk); // Count up to 65535
    #10;
    $display("16-bit Count (Overflow): %h", count_16bit); // Should be FFFF (65535)
    #10;
    $display("16-bit Count (After Overflow): %h", count_16bit); // Should be 0000 (wrapped around)

    $finish;
  end

endmodule

Program Counter

The program_counter module:

module program_counter #(
  parameter WIDTH = 8 // Default width of 8 bits
) (
  input logic clk,
  input logic rst,
  input logic enable,
  input logic load,          // Load a new PC value
  input logic [WIDTH-1:0] load_value, // Value to load
  output logic [WIDTH-1:0] pc      // Program counter output
);

  always_ff @(posedge clk) begin
    if (rst) begin
      pc_internal <= '0; // Reset to 0
    end else if (enable) begin
      if (load) begin
        pc_internal <= load_value; // Load new value
      end else begin
        pc_internal <= pc_internal + 1; // Increment PC
      end
    end
  end

  assign pc = pc_internal; // Assign internal value to output

endmodule

The test bench for program_counter:

// Testbench for program counter
module program_counter_tb;
  logic clk;
  logic rst;
  logic enable;
  logic load;
  logic [7:0] load_value;
  logic [7:0] pc;

  // Instantiate the program counter (default 8-bit width)
  program_counter pc_8bit (
    .clk(clk),
    .rst(rst),
    .enable(enable),
    .load(load),
    .load_value(load_value),
    .pc(pc)
  );

    // Instantiate a 16-bit PC for testing parameter override.
  logic [15:0] load_value_16bit;
  logic [15:0] pc_16bit;
  program_counter #(16) pc_16bit_inst (
    .clk(clk),
    .rst(rst),
    .enable(enable),
    .load(load),
    .load_value(load_value_16bit),
    .pc(pc_16bit)
  );


  // Clock generation
  initial begin
    clk = 0;
    forever #5 clk = ~clk;
  end

  // Test sequence
  initial begin
    rst = 1;
    enable = 0;
    load = 0;

    #10 rst = 0; // Release reset
    enable = 1;

    #10; // pc should now be 1

    load = 1;
    load_value = 8'hFF;
    load_value_16bit = 16'hFFFF;
    #10 load = 0; // Deactivate load

    #10; // pc should now be FF (8 bit) and FFFF (16 bit)

    #10; // pc should now be 00 (8 bit) and 0000 (16 bit) because of overflow

    $display("8-bit PC: %h", pc);       // Should be FF
    $display("16-bit PC: %h", pc_16bit); // Should be FFFF

    $finish;
  end

endmodule

Sign Extender

The sign_extender module:

module sign_extender #(
  parameter IN_WIDTH = 16, // Input width (default 16 bits)
  parameter OUT_WIDTH = 32 // Output width (default 32 bits)
) (
  input logic [IN_WIDTH-1:0] in,
  output logic [OUT_WIDTH-1:0] out
);

  // Sign extension logic: replicate the most significant bit of the input
  // to fill the additional bits in the output.
  assign out = , in}; 

endmodule

The test bench for the sign_extender module:

// Testbench for sign extender
module sign_extender_tb;
  logic [15:0] in;
  logic [31:0] out;

  // Instantiate the sign extender (default parameters)
  sign_extender se_16_to_32 (
  .in(in),
  .out(out)
  );

  // Instantiate a sign extender with different parameters (e.g., 8 to 32)
  logic [7:0] in_8;
  logic [31:0] out_8;
  sign_extender #(8, 32) se_8_to_32 (
  .in(in_8),
  .out(out_8)
  );

  initial begin
    // Test cases
    in = 16'h7FFF; // Positive number
    #10;
    $display("16-bit input: %h, 32-bit output: %h", in, out); // Expected: 00007FFF

    in = 16'h8000; // Negative number (MSB is 1)
    #10;
    $display("16-bit input: %h, 32-bit output: %h", in, out); // Expected: FFFF8000

    in = 16'hFFFF; // -1
    #10;
    $display("16-bit input: %h, 32-bit output: %h", in, out); // Expected: FFFFFFFF

    in_8 = 8'h7F; // Positive number
    #10;
    $display("8-bit input: %h, 32-bit output (8 to 32): %h", in_8, out_8); // Expected: 0000007F

    in_8 = 8'h80; // Negative number
    #10;
    $display("8-bit input: %h, 32-bit output (8 to 32): %h", in_8, out_8); // Expected: FFFFFFF80

    $finish;
  end

endmodule

Shift Logical Left (sll) or Right (slr)

Shift Logical Left sll

The shift_left module:

module shift_left #(
  parameter WIDTH = 8, // Default width of 8 bits
  parameter SHIFT_AMOUNT = 1 // Default shift amount of 1
) (
  input logic [WIDTH-1:0] data_in,
  output logic [WIDTH-1:0] data_out
);

  // Shift left by SHIFT_AMOUNT (logical shift)
  assign data_out = data_in << SHIFT_AMOUNT;

endmodule

The test bench for the shift_left module:

// Testbench for shift left module
module shift_left_tb;
  logic [7:0] data_in;
  logic [7:0] data_out;

  // Instantiate the shift left module (default parameters)
  shift_left sl_8bit (
.data_in(data_in),
.data_out(data_out)
  );

  // Instantiate a shift left module with different parameters
  logic [15:0] data_in_16bit;
  logic [15:0] data_out_16bit;
  shift_left #(16, 2) sl_16bit ( // 16-bit width, shift by 2
.data_in(data_in_16bit),
.data_out(data_out_16bit)
  );

  initial begin
    // Test cases for 8-bit shift
    data_in = 8'h01; // 0000 0001
    #10;
    $display("8-bit input: %h, output: %h", data_in, data_out); // Expected: 0000 0010 (shift by 1)

    data_in = 8'h80; // 1000 0000
    #10;
    $display("8-bit input: %h, output: %h", data_in, data_out); // Expected: 0000 0000 (shift by 1 - logical)

    data_in = 8'h0F; // 0000 1111
    #10;
    $display("8-bit input: %h, output: %h", data_in, data_out); // Expected: 0001 1110 (shift by 1)


    // Test cases for 16-bit shift
    data_in_16bit = 16'h0001; // 0000 0000 0000 0001
    #10;
    $display("16-bit input: %h, output: %h", data_in_16bit, data_out_16bit); // Expected: 0000 0000 0000 0100 (shift by 2)

    data_in_16bit = 16'h8000; // 1000 0000 0000 0000
    #10;
    $display("16-bit input: %h, output: %h", data_in_16bit, data_out_16bit); // Expected: 0000 0000 0000 0000 (shift by 2 - logical)

    $finish;
  end

endmodule

Shift Logical Right slr

The shift_right module:

module shift_right #(
  parameter WIDTH = 8, // Default width of 8 bits
  parameter SHIFT_AMOUNT = 1 // Default shift amount of 1
) (
  input logic [WIDTH-1:0] data_in,
  output logic [WIDTH-1:0] data_out
);

  // Logical shift right by SHIFT_AMOUNT
  assign data_out = data_in >> SHIFT_AMOUNT;

endmodule

The test bench for the shift_right module:

// Testbench for shift right logical module
module shift_right_tb;
  logic [7:0] data_in;
  logic [7:0] data_out;

  // Instantiate the shift right logical module (default parameters)
  shift_right srl_8bit (
  .data_in(data_in),
  .data_out(data_out)
  );

  // Instantiate a shift right logical module with different parameters
  logic [15:0] data_in_16bit;
  logic [15:0] data_out_16bit;
  shift_right #(16, 2) srl_16bit ( // 16-bit width, shift by 2
  .data_in(data_in_16bit),
  .data_out(data_out_16bit)
  );

  initial begin
    // Test cases for 8-bit shift
    data_in = 8'h01; // 0000 0001
    #10;
    $display("8-bit input: %h, output: %h", data_in, data_out); // Expected: 0000 0000 (shift by 1)

    data_in = 8'h80; // 1000 0000
    #10;
    $display("8-bit input: %h, output: %h", data_in, data_out); // Expected: 0100 0000 (shift by 1 - logical)

    data_in = 8'hFF; // 1111 1111
    #10;
    $display("8-bit input: %h, output: %h", data_in, data_out); // Expected: 0111 1111 (shift by 1)

        data_in = 8'h0F; // 0000 1111
    #10;
    $display("8-bit input: %h, output: %h", data_in, data_out); // Expected: 0000 0111 (shift by 1)


    // Test cases for 16-bit shift
    data_in_16bit = 16'h0001; // 0000 0000 0000 0001
    #10;
    $display("16-bit input: %h, output: %h", data_in_16bit, data_out_16bit); // Expected: 0000 0000 0000 0000 (shift by 2)

    data_in_16bit = 16'h8000; // 1000 0000 0000 0000
    #10;
    $display("16-bit input: %h, output: %h", data_in_16bit, data_out_16bit); // Expected: 0010 0000 0000 0000 (shift by 2 - logical)

        data_in_16bit = 16'hFFFF; // 1111 1111 1111 1111
    #10;
    $display("16-bit input: %h, output: %h", data_in_16bit, data_out_16bit); // Expected: 0011 1111 1111 1111 (shift by 2)

    $finish;
  end

endmodule

Difference between Shift Logical & Shift Arithmetic

A crucial difference between logical and arithmetic shift operations exists, particularly when dealing with signed numbers.

Let’s break it down:

Logical Shift:

Arithmetic Shift:

Why the Difference Matters (Signed Numbers):

The key difference arises with right shifts of signed numbers.

Shift Type Left Shift Right Shift
Logical Zeros in from the right Zeros in from the left
Arithmetic Zeros in from the right (same as logical) Sign bit (MSB) is copied and filled in from left

Finite State Machines (FSM) in SystemVerilog

Mealy FSM

A simple Mealy FSM mealy_fsm module:

module mealy_fsm #(
  parameter NUM_STATES = 4 // Example: 4 states
) (
  input logic clk,
  input logic rst,
  input logic in,
  output logic out
);

  // Define the states (using an enum is good practice)
  typedef enum logic [1:0] { S0 = 2'b00, S1 = 2'b01, S2 = 2'b10, S3 = 2'b11 } state_type;

  state_type current_state, next_state;

  // State register (sequential logic)
  always_ff @(posedge clk) begin
    if (rst) begin
      current_state <= S0; // Reset to initial state (S0)
    end else begin
      current_state <= next_state;
    end
  end

  // Next state logic (combinational)
  always_comb begin
    next_state = current_state; // Default: stay in the current state

    case (current_state)
      S0: begin
        if (in) next_state = S1;
      end
      S1: begin
        if (in) next_state = S2;
      end
      S2: begin
        if (in) next_state = S3;
      end
      S3: begin
        if (in) next_state = S0;
      end
    endcase
  end

  // Output logic (combinational - Mealy output depends on current state *and* input)
  always_comb begin
    out = 0; // Default output

    case (current_state)
      S0: begin
        if (in) out = 1;
      end
      S1: begin
        if (in) out = 0;
      end
      S2: begin
        if (in) out = 1;
      end
      S3: begin
        if (in) out = 0;
      end
    endcase
  end

endmodule

The test bench for the simple Mealy FSM mealy_fsm module:

// Testbench for Mealy FSM
module mealy_fsm_tb;
  logic clk;
  logic rst;
  logic in;
  logic out;

  mealy_fsm fsm (
  .clk(clk),
  .rst(rst),
  .in(in),
  .out(out)
  );

  // Clock generation
  initial begin
    clk = 0;
    forever #5 clk = ~clk;
  end

  // Test sequence
  initial begin
    rst = 1;
    in = 0;

    #10 rst = 0; // Release reset

    in = 1; // Input 1
    #10;
    $display("State: %s, Input: %b, Output: %b", fsm.current_state, in, out); // Expected: S1, 1, 1

    in = 1; // Input 1
    #10;
    $display("State: %s, Input: %b, Output: %b", fsm.current_state, in, out); // Expected: S2, 1, 0

    in = 1; // Input 1
    #10;
    $display("State: %s, Input: %b, Output: %b", fsm.current_state, in, out); // Expected: S3, 1, 1

    in = 1; // Input 1
    #10;
    $display("State: %s, Input: %b, Output: %b", fsm.current_state, in, out); // Expected: S0, 1, 0


    in = 0; // Input 0
    #10;
    $display("State: %s, Input: %b, Output: %b", fsm.current_state, in, out); // Expected: S0, 0, 0 (No state change because input is 0)

    $finish;
  end

endmodule

Moore FSM

A simple Moore FSM moore_fsm module:</summary>

module moore_fsm #(
  parameter NUM_STATES = 4 // Example: 4 states
) (
  input logic clk,
  input logic rst,
  input logic in,
  output logic out
);

  // Define the states (using an enum is good practice)
  typedef enum logic [1:0] { S0 = 2'b00, S1 = 2'b01, S2 = 2'b10, S3 = 2'b11 } state_type;

  state_type current_state, next_state;

  // State register (sequential logic)
  always_ff @(posedge clk) begin
    if (rst) begin
      current_state <= S0; // Reset to initial state (S0)
    end else begin
      current_state <= next_state;
    end
  end

  // Next state logic (combinational)
  always_comb begin
    next_state = current_state; // Default: stay in the current state

    case (current_state)
      S0: begin
        if (in) next_state = S1;
      end
      S1: begin
        if (in) next_state = S2;
      end
      S2: begin
        if (in) next_state = S3;
      end
      S3: begin
        if (in) next_state = S0;
      end
    endcase
  end

  // Output logic (combinational - Moore output depends *only* on current state)
  always_comb begin
    out = 0; // Default output

    case (current_state)
      S0: out = 0;
      S1: out = 1;
      S2: out = 0;
      S3: out = 1;
    endcase
  end

endmodule

The test bench for the simple Moore FSM moore_fsm module:

// Testbench for Moore FSM
module moore_fsm_tb;
  logic clk;
  logic rst;
  logic in;
  logic out;

  moore_fsm fsm (
  .clk(clk),
  .rst(rst),
  .in(in),
  .out(out)
  );

  // Clock generation
  initial begin
    clk = 0;
    forever #5 clk = ~clk;
  end

  // Test sequence
  initial begin
    rst = 1;
    in = 0;

    #10 rst = 0; // Release reset

    in = 1; // Input 1
    #10;
    $display("State: %s, Input: %b, Output: %b", fsm.current_state, in, out); // Expected: S1, 1, 1

    in = 1; // Input 1
    #10;
    $display("State: %s, Input: %b, Output: %b", fsm.current_state, in, out); // Expected: S2, 1, 0

    in = 1; // Input 1
    #10;
    $display("State: %s, Input: %b, Output: %b", fsm.current_state, in, out); // Expected: S3, 1, 1

    in = 1; // Input 1
    #10;
    $display("State: %s, Input: %b, Output: %b", fsm.current_state, in, out); // Expected: S0, 1, 0


    in = 0; // Input 0
    #10;
    $display("State: %s, Input: %b, Output: %b", fsm.current_state, in, out); // Expected: S0, 0, 0 (No state change because input is 0)

    $finish;
  end

endmodule

What is Computer Architecture?

Welcome to Computer Architecture! This course will delve into the fundamental principles governing how computers work at a hardware level. It’s not just about programming (though that’s related!), nor is it solely about circuit design (though that plays a role). Computer architecture sits at the intersection of hardware and software, defining the interface between them.

Think of it as the blueprint of a building, like our New Academic Building. Architects don’t lay every brick, nor do they decide how the occupants will use each room. Instead, they design the structure, layout, and systems (electrical, plumbing) that enable both construction and habitation. Similarly, computer architects define the fundamental organization and behavior of a computer system, enabling both hardware implementation and software execution.

Key Questions to Consider

Why Study Computer Architecture?

The Five Classic Components of a Computer

Every computer, from your smartphone to a supercomputer, can be conceptually broken down into five main components:

  1. Input: Mechanisms for feeding data into the computer (keyboard, mouse, network interface, sensors, etc.).
  2. Output: Mechanisms for displaying or transmitting results (monitor, printer, network interface, actuators, etc.).
  3. Memory: Stores both instructions (the program) and data that the computer is actively using. Think of it as the computer’s workspace. We’ll explore different types of memory (RAM, cache, registers) in detail later.
  4. Arithmetic Logic Unit (ALU): Performs the actual computations (arithmetic operations, logical comparisons) on the data. This is the “brain” of the CPU.
  5. Control Unit: Directs the operation of all other components. It fetches instructions from memory, decodes them, and issues signals to the ALU, memory, and I/O devices to execute those instructions. It’s the “conductor” of the computer’s orchestra.

These five components are interconnected by buses, which are sets of wires that carry data and control signals.

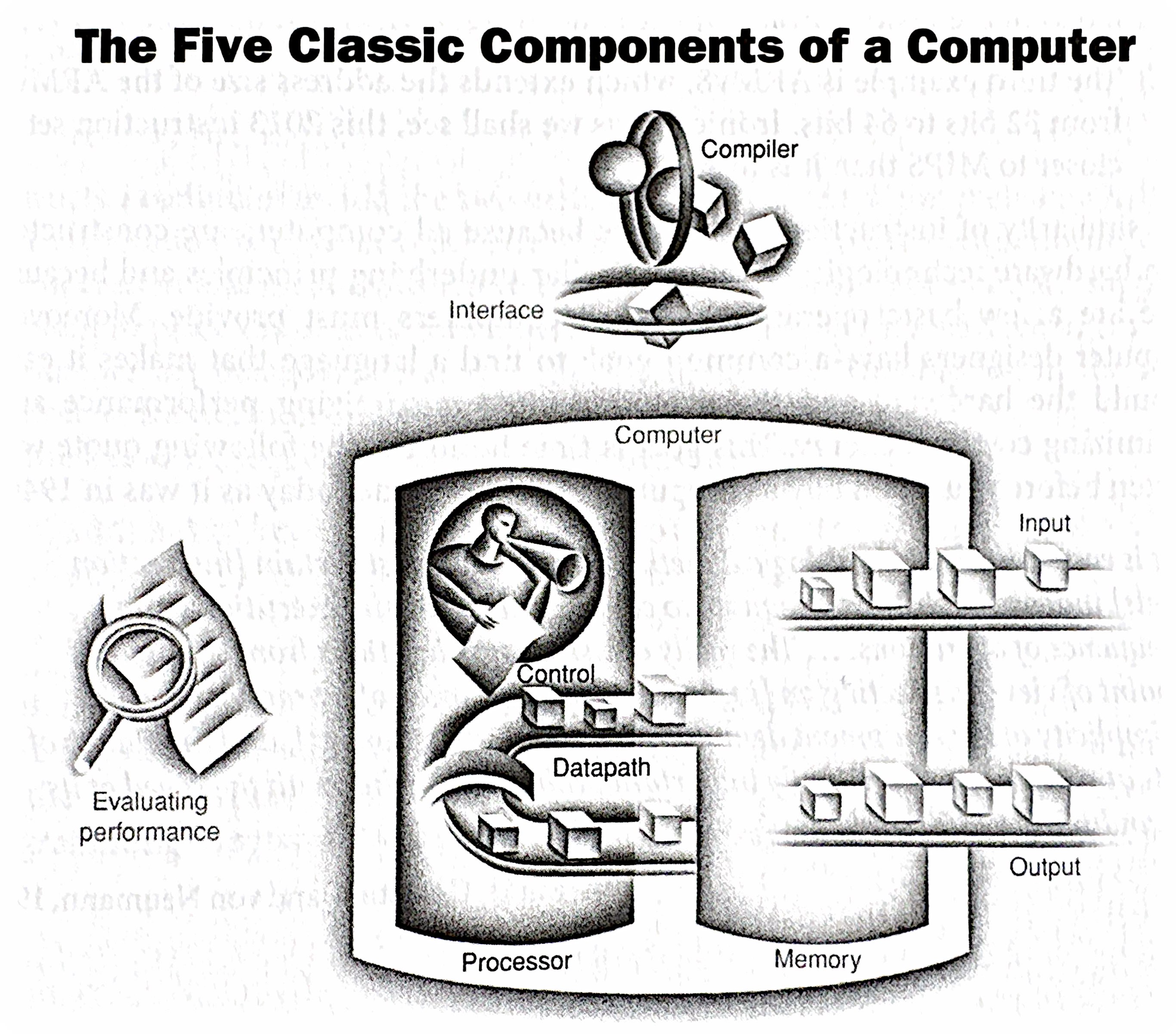
Five Components

The Stored Program Concept

One of the most crucial concepts in computer architecture is the stored program concept. Before this, computers were often hardwired for specific tasks. Changing the program required rewiring the machine—a tedious and error-prone process.

The stored program concept, attributed to John von Neumann, revolutionized computing by storing both the instructions (the program) and the data in the computer’s memory. This allows for:

This concept is fundamental to how all modern computers operate.

IV. von Neumann vs. Harvard Architectures

While the von Neumann architecture is dominant, it’s important to understand its historical context and alternatives.

Feature Von Neumann (Princeton) Architecture Harvard Architecture
Memory Single memory space for both instructions and data Separate memory spaces for instructions and data
Access Instructions and data share the same memory bus Instructions and data can be accessed simultaneously
Advantages Simpler design, more efficient use of memory Faster instruction fetch, avoids bottlenecks
Disadvantages Potential bottleneck (von Neumann bottleneck) as both instructions and data compete for the same memory access More complex design, requires separate memory modules
Applications General-purpose computers, PCs, laptops Embedded systems, digital signal processors (DSPs)

The von Neumann bottleneck arises because both instructions and data must travel over the same bus to and from memory. This can limit performance, especially when the CPU needs to fetch instructions and data frequently. The Harvard architecture mitigates this by allowing parallel access to instruction and data memories.

(Diagrams comparing the two architectures)

While modern general-purpose computers primarily use variations of the von Neumann architecture (often with caching and other techniques to reduce the bottleneck), the Harvard architecture is still relevant in specialized applications where performance and parallelism are critical.

Additional readings for these architecture types:

Introducing Performance of a Computer

Background reading on performance

Defining Performance in Computer Architecture

Performance in computer architecture is a multifaceted concept, and there isn’t one single “best” metric. It’s often a balancing act between different factors, and the “right” performance measure depends on the specific application and priorities. Here’s a breakdown of key aspects:

1. Execution Time:

2. Throughput:

3. Latency:

4. Resource Utilization:

5. Power Consumption:

6. Cost:

Sidebar — The Power Wall in Computer Architecture

The “Power Wall” refers to the increasing difficulty and impracticality of continuing to increase processor clock speeds to achieve performance gains. For many years, increasing clock speed was the primary driver of improved CPU performance. However, this approach has run into fundamental physical limitations, leading to the “power wall.”

The Problem:

As clock speeds increase, so does the power consumption of the processor. This increased power consumption manifests as heat. The relationship is roughly cubic: doubling the clock speed can increase power consumption by a factor of eight. This heat becomes increasingly difficult and expensive to dissipate. Think of it like trying to cool a rapidly boiling pot of water; at some point, you can’t add any more heat without it boiling over.

Consequences of Excessive Heat:

The Relationship Between Clock Speed and Power

Where:

Why It’s Close to a Factor of Eight

  1. Linear Increase with Frequency: If you only doubled the clock speed and kept the voltage the same, the power would increase linearly (doubling).
  2. Voltage Increase: However, to reliably double the clock speed, you typically need to increase the voltage. This increase in voltage, when squared, has a much larger impact on power consumption.
  3. Combined Effect: The combination of the linear increase from frequency and the quadratic increase from voltage results in a power increase that is close to a factor of eight when you double the clock speed.

Important Caveats

In Summary

While not an absolute rule, the “factor of eight” is a good rule of thumb to illustrate the significant power challenges associated with increasing clock speeds. It highlights the need for innovative design techniques and power management strategies in modern computer architecture.

The Shift in Focus:

The power wall has forced a fundamental shift in how computer architects design processors. Instead of focusing solely on increasing clock speed, the emphasis has moved towards:

In summary: The power wall is a critical challenge in computer architecture. It signifies the limitations of simply increasing clock speeds to achieve performance gains. The industry has responded by shifting its focus towards multi-core processors, specialized hardware, architectural innovations, and power-efficient designs. Managing power consumption and heat dissipation has become a central concern for computer architects.

Looking Ahead to next lecture — Instruction Set Architecture (ISA)

Today, we’ve laid the foundation for understanding the basic components and principles of computer architecture. Our next lecture will delve into the Instruction Set Architecture (ISA).

The ISA defines the set of instructions that a particular processor can understand and execute. It’s the interface between the hardware and the software. We’ll explore:

Understanding the ISA is crucial for writing efficient code, optimizing compiler design, and designing new processors. It’s the bridge between the high-level world of programming and the low-level world of hardware.

← back to syllabus ← back to notes

This site built with GitHub.